Programmer un jeu de réflexion « Christophe Blaess

Programmer un jeu de réflexion

Janvier 2003

Cet article se propose d’offrir une introduction aux techniques d’Intelligence Artificielle les plus simples que l’on utilise pour la résolution des jeux de réflexion. Cette présentation vous donnera envie, espèrons-le, de mettre en pratique ces concepts, en programmant vous-même des jeux de réflexion, existants ou inventés pour l’occasion. Nous allons nous intéresser ici à un passionnant jeu de stratégie d’origine africaine : l’Awélé.

Le jeu d’Awélé

L’Awélé fait partie de la famille des jeux de semaille, où des graines circulent alternativement sur les domaines des deux adversaires, et où la victoire revient à celui dont la récolte est la plus avantageuse. Appartenant à une culture de tradition orale, l’Awélé est un jeu vivant, dont les règles évoluent selon les régions et selon les époques. Nous utiliserons les règles les plus communément admises, mais des variations sont donc tout à fait imaginables.

L’Awélé se joue sur un plateau où sont creusés douze trous, organisés en deux rangées appartenant aux deux adversaires. On place initialement quatre graines dans chaque trou. Les trous peuvent être simplement creusés dans le sable et les graines figurées par de petits cailloux, ou au contraire le plateau peut être une oeuvre d’art richement décorée. Alternativement, chaque joueur saisit tout le contenu de l’un de ses propres trous et le sème, graine par graine, dans le sens inverse des aiguilles d’une montre, dans chaque trou – y compris ceux de son adversaire. La seule exception est le trou de départ qui, stérile pendant une saison, doit rester vide. Il est donc sauté lors de la semaille. Lorsque la dernière graine est posée dans un trou de l’adversaire comportant préalablement une ou deux graines, le contenu de ce trou peut être capturé, c’est-à-dire mis en réserve hors du jeu. De plus tous les trous précédents de l’adversaire répondant aux mêmes critères (contenant après semis deux ou trois graines) peuvent également être capturés. Les graines ne ressortent pas de la réserve, elles seront seulement comptabilisées pour déterminer le vainqueur.

Le but de l’Awélé est une domination économique et non pas une victoire guerrière, contrairement aux autres principaux jeux de stratégie comme le Go ou les échecs. Aussi est-il interdit d’affamer l’adversaire : on doit toujours lui laisser au moins une graine dans son camps. Si c’est impossible, la partie se termine. Le vainqueur est le joueur qui a mis le plus de graines en réserve. En pratique, la fin de la partie est généralement déterminée bien avant d’en arriver à cette extrémité, puisque dès qu’un joueur possède plus de vingt-quatre graines dans sa réserve, il ne peut plus être dépassé.

L’Awélé est un jeu complexe, comportant des retournements de situation très rapides, et nécessitant une dose importante de calculs et de stratégies, reposant entre autres sur la constitution de « greniers », c’est-à-dire de trous comportant un nombre important de graines (une vingtaine par exemple). Pour un joueur débutant toutefois, l’ordinateur peut représenter un adversaire intéressant par sa faculté d’explorer rapidemment un nombre important de combinaisons.

Résolution de jeux

L’Intelligence Artificielle est une branche de l’informatique recouvrant de très nombreux domaines d’application, (reconnaissance des formes, expertise et diagnostique automatiques, modélisation, logiques, traitement du langage, etc.) mais l’un de ses sujets de prédilection fut dès ses débuts la résolution des jeux de réflexion. Des mécanismes divers ont été mis au point à cette fin, mais le plus courant, et le plus simple à comprendre, est l’exploration en force brute. Il s’agit, partant d’une position de jeu, de tester successivement tous les mouvements possibles, puis pour chacun d’eux tous les mouvements de l’adversaire, en itérant le processus pour déterminer quel mouvement immédiat est le plus à même de nous apporter finalement la victoire.

Pour certains jeux, comme le tic-tac-toe à neuf cases, le nombre de situations est suffisament faible pour être exploré entièrement par un ordinateur (et même par un humain compte tenu des symétries réduisant considérablement le nombre de branches à étudier). En revanche, pour un jeu offrant une certaine complexité, l’exploration exhaustive est impossible pour des raisons d’explosion combinatoire. On a recours alors à une fonction d’évaluation. On commence l’exploration de tous les mouvements possibles, puis de tous ceux de l’adversaire, et ainsi de suite jusqu’à une profondeur maximale. La situation résultante est soumise à une fonction qui va la noter, lui affectant une valeur positive si elle nous est favorable, ou négative si elle est favorable à l’adversaire.

L’idée consiste alors à faire « remonter » jusqu’à la position de départ les notes obtenues pour chaque séquence de mouvements, afin de déterminer le mouvement initial le plus intéressant. Considérant que l’adversaire joue aussi bien que nous, la remontée des notes s’effectue en utilisant un algorithme nommé minimax, qui prend alternativement le coup le plus favorable (lorsque nous jouons) et le plus défavorable (lorsque l’autre joue). Cet algorithme peut s’exprimer de différentes manières, en voici une représentation récursive :

minimax (position, joueur, profondeur)
  si profondeur = profondeur_maximale
    renvoyer evaluation (position)
  pour tous les mouvements possibles
      nouvelle = appliquer_mouvement (position, mouvement)
      valeur = minimax (nouvelle, adversaire(joueur), profondeur+1)
  si joueur = "nous"
    renvoyer maximum des valeurs
  sinon
    renvoyer minimum des valeurs

En supposant que la fonction d’évaluation accepte un argument indiquant pour quel joueur elle doit être calculée (et donc le sens positif ou négatif qu’elle doit prendre), on peut simplifier l’expression de l’algorithme ainsi :

minimax (position, joueur, profondeur)
  si profondeur = profondeur_maximale
    renvoyer evaluation(position, joueur)
  maximum = -infini
  pour tous les mouvements possibles (adversaire(joueur))
    nouvelle = appliquer_mouvement(position, mouvement)
    valeur = - minimax(nouvelle, adversaire(joueur), profondeur+1)
    si valeur > maximum
      maximum = valeur
  renvoyer maximum

En fait, toute l’intelligence du système repose finalement dans la fonction d’évaluation, qui doit indiquer – avec la meilleure précision possible – l’avantage qu’offre une position pour un joueur donné. Nous reviendrons sur ce sujet.

Comme c’est fréquemment le cas en IA, on représente usuellement le principe de résolution des jeux par un arbre. On déplace ainsi les problèmes, en les ramenant à des manipulations (parcours, tri, etc.) de graphes pour lesquels on dispose de nombreux algorithmes. Chaque noeud de l’arbre représente une position du jeu, et chaque arc qui en sort est assimilé à un mouvement menant à une nouvelle position. à chaque tour de jeu, il y a, au plus, six mouvements possibles (chacun des six trous). Ceci est très faible en regard d’autres jeux comme les échecs qui peuvent en proposer plusieurs dizaines, ou le Go qui peut atteindre plusieurs centaines ! L’arbre à explorer sera donc relativement « pointu », et l’on essayera de privilégier la profondeur de la descente.

Pour cela, il existe une technique nommée élagage alpha-béta. Il s’agit d’améliorer l’algorithme en renonçant à étudier les mouvements ne permettant pas d’améliorer le résultat déja obtenu pour une position donnée. Sachant qu’à partir d’une position, on a déjà atteint une certaine valeur grâce aux mouvements explorés, il est inutile d’examiner plus longuement les mouvements ne permettant pas de monter au-dessus de cette valeur. Or, au tour suivant c’est l’adversaire qui joue, et en tentant de maximiser son avantage, il diminue le nôtre, et l’exploration de ce niveau ne pourra que faire diminuer l’avantage obtenu au niveau supérieur.

Il est facile d’exprimer l’élagage alpha-béta dans un algorithme utilisant une fonction d’évaluation symétrique comme nous l’avons fait plus haut. En effet, lorsqu’on invoque minimax(), on lui transmet un argument supplémentaire correspondant à l’opposé de la meilleur valeur déja obtenue à notre niveau. Si l’exploration au niveau suivant dépasse cet argument, son opposé sera nécessairement inférieur à la valeur déjà obtenue, et il n’est pas utile d’étudier les autres mouvements.

minimax (position, joueur, profondeur,alpha)
  si profondeur = profondeur_maximale
    renvoyer evaluation(position, joueur)
  maximum = -infini
  pour tous les mouvements possibles (adversaire(joueur))
    nouvelle = appliquer_mouvement(position, mouvement,maximum)
    valeur = - minimax(nouvelle, adversaire(joueur), profondeur+1, -maximum)
    si valeur > maximum
      maximum = valeur
    si valeur > alpha
      sortir boucle pour
  renvoyer maximum

Pour bien saisir le fonctionnement de l’algorithme minimax et l’élagage alpha-béta, il est recommandé de le faire « tourner » manuellement sur un arbre construit pour l’occasion. On trouvera également des explications plus claires et plus détaillées dans de nombreux ouvrages d’introduction à l’IA comme [WINSTON 92] ou à l’algorithmique, comme [GOLDSCHLAGER 86] par exemple.

Implémentation

Algorithme minimax

L’implémentation d’un algorithme minimax est relativement simple. Il faut d’abord trouver une bonne représentation de l’état du jeu. Pour l’Awélé, il suffit d’employer un tableau de deux fois six cases, plus deux cases contenant les graines capturées. Il faut ensuite choisir un langage de développement. Ici, nous ferons preuve d’originalité, en nous tournant vers le langage Tcl, ceci pour trois raisons :

en tant que langage de script, Tcl est simple à lire et à programmer, la traduction de l’algorithme exprimé ci-dessus se fera très facilement ;
l’interpréteur Tcl est disponible sur toutes les plateformes Unix et la bibliothèque Tk livrée avec lui nous permettra de disposer très facilement d’une interface graphique pour le jeu ;
enfin, il est toujours amusant d’essayer d’employer un langage au-delà de ses limites habituelles. Tcl est souvent utilisé comme un langage de regroupement de commande (une sorte de super script shell), mais rarement pour de véritables programmes de calcul. Démontrons donc qu’il en est capable !

Pour les lecteurs désireux de s’initier au langage Tcl ou à l’utilisation de la bibliothèque Tk, je ne peux que vous conseiller la lecture de [BLAESS 01] !

L’interpréteur Tcl étant livré avec toutes les distributions Linux, aucun problème ne devrait se poser pour tester les routines ci-dessous. La première routine que nous examinerons est le coeur même de l’algorithme minimax. On peut d’ailleurs presque reconnaître ligne-à-ligne son expression ci-dessus.

proc evaluation_mouvement {ref_jeu joueur profondeur mvt alpha} {
  upvar $ref_jeu jeu
  global profondeur_maxi liste_mouvements erreur
  if {[effectuer_mouvement jeu $joueur $mvt] < 0} {return $erreur}
  if {[incr profondeur] >= $profondeur_maxi} {
    return [evaluation_position jeu $joueur]
  }
  set joueur [expr 1 - $joueur]
  set meilleure_evaluation $erreur
  foreach mvt $liste_mouvements {
    array set copie_jeu  [array get jeu]
    set valeur [evaluation_mouvement copie_jeu $joueur $profondeur $mvt [expr - $meilleure_evaluation]]
    if {$valeur == $erreur} {continue}
    set valeur [expr - $valeur]
    if {$valeur > $meilleure_evaluation} {
      set meilleure_evaluation $valeur
      if {$valeur > $alpha} {break}
    }
  }
  return $meilleure_evaluation;
}

La première instruction de cette routine – upvar – indique que le premier argument est une référence symbolique, ou plus précisément le nom d’une variable appartenant à la routine appelante. C’est donc le moyen employé en Tcl pour passer des arguments par référence. Le tableau jeureprésente le contenu des différents trous. jeu(0,…) correspond au joueur Nord (par défaut l’ordinateur) et jeu(1,…) au joueur Sud. Pour chacun d’eux, jeu(…,i) avec i dans [0,6[ correspondent aux six trous, numérotés dans l’ordre inverse des aiguilles d’une montre. Enfinjeu(0,6) et jeu(1,6) correspondent aux deux réserves de graines capturées. La numérotation des trous est représentée sur le tableau ci-dessous.

jeu(0,6)	jeu(0,5)	jeu(0,4)	jeu(0,3)	jeu(0,2)	jeu(0,1)	jeu(0,0)	jeu(1,6)
jeu(0,6)	jeu(1,0)	jeu(1,1)	jeu(1,2)	jeu(1,3)	jeu(1,4)	jeu(1,5)	jeu(1,6)

Il est important de remarquer que les premières routines que nous développons considèrent la variable jeu dans son ensemble comme une représentation de la situation, sans faire référence à son contenu. Nous pourrons réutiliser ces fonctions directement avec d’autres jeux de réflexion.

Nous pouvons remarquer l’existence des variables globales suivantes :

profondeur_maxi : le nombre de niveaux à explorer dans l’arbre des possibilités, chaque niveau de cet arbre correspondant à un demi-coup ;
liste_mouvements : une liste contenant tous les mouvements possibles pour chaque joueur. Ici il ne s’agit que de la liste {0 1 2 3 4 5} correspondant aux six trous ;
erreur : il s’agit d’une valeur numérique qui doit être inférieure à la pire des évaluations possibles. Nous choisissons arbitrairement -100000.

La routine effectuer_mouvement devra appliquer le mouvement désiré au jeu, et renvoyer une valeur négative en cas d’impossibilité. Nous voyons que le reste de la fonction est assez proche de l’algorithme précédent, avec quelques remarques :

La boucle foreach permet de balayer la liste des mouvements de manière plus lisible qu’une boucle for ;
L’instruction Tcl array permet de manipuler les tableaux, nous l’utilisons ici pour dupliquer la table représentant le jeu.

Nous savons donc évaluer un mouvement donné. Nous devrons utiliser une routine permettant de déterminer le meilleur mouvement pour une position de départ donné. Cette fonction s’écrit de manière assez évidente.

proc meilleur_mouvement {ref_jeu joueur} {
  upvar $ref_jeu jeu
  global liste_mouvements erreur
  set meilleure_evaluation $erreur
  set meilleur $erreur
  foreach mvt $liste_mouvements {
    array set copie_jeu  [array get jeu]
    set valeur [evaluation_mouvement copie_jeu $joueur 0 $mvt [expr - $erreur]]
    if {$valeur == $erreur} {continue}
      if {$valeur > $meilleure_evaluation} {
        set meilleure_evaluation $valeur
        set meilleur $mvt
    }
  }
  return $meilleur
}

On notera que si aucun mouvement n’est acceptable, elle renvoie la valeur d’erreur.

Routines de jeu

Nous pouvons à présent écrire les routines encadrant le déroulement la partie. Il nous faut disposer d’une variable globale stockant le numéro du joueur en cours. La première routine correspond au jeu de l’ordinateur.

proc ordinateur_joue {ref_jeu} {
  upvar $ref_jeu jeu
  global joueur_en_cours erreur
  set mvt [meilleur_mouvement jeu $joueur_en_cours]
  if {$mvt == $erreur} {
    afficher_resultats jeu
  } else {
    effectuer_mouvement jeu $joueur_en_cours $mvt
    afficher_jeu jeu
    indiquer_coup_joue $joueur_en_cours $mvt
    passer_la_main
    if [partie_terminee jeu] {afficher_resultats jeu ; return}
  }
}

Nous voyons qu’elle invoque plusieurs routines concernant l’interface graphique (comme afficher_resultats, afficher_jeu, indiquer_coup_joue, passer_la_main). Elles seront développées plus bas. La routine suivante est invoquée lorsque l’humain demande à jouer un certain trou. Elle vérifie que le mouvement soit correct en passant par une copie intermédiaire du jeu.

proc humain_joue {ref_jeu j c} {
  upvar $ref_jeu jeu
  global joueur_en_cours
  if {$j != $joueur_en_cours} { bell; return }
  array set copie [array get jeu]
  if {[effectuer_mouvement copie $j $c] < 0} {bell; return}
  array set jeu [array get copie]
  afficher_jeu jeu
  passer_la_main
  if [partie_terminee jeu] {afficher_resultats jeu ; return}
  after 10 ordinateur_joue jeu
}

La dernière ligne de cette routine lance la réflexion de l’ordinateur au bout de 10 millisecondes. Cet intervalle permet à la bibliothèque Tk de traiter sa boucle d’évènements, rafraichissant ainsi l’affichage graphique.

Nous avons besoin d’une routine permettant de basculer d’un joueur à l’autre. Elle met à jour la variable globale concernée et invoque la fonction d’interface s’occupant de l’affichage du nom du joueur attendu.

proc passer_la_main {} {
  global joueur_en_cours
  set joueur_en_cours [expr 1 - $joueur_en_cours]
  afficher_joueur_en_cours $joueur_en_cours
}

Jeu d’Awélé

Jusqu’à présent, les fonctions développées sont totalement indépendantes du jeu implémenté, nous pourrions les employer pour un grand nombre de jeux de réflexion. Voyons maintenant les fonctions spécifiques au jeu d’Awélé. Tout d’abord, la fonction initialisant toutes les données du jeu, conformément au tableau suivant :

jeu(j,i)	i=0	i=1	i=2	i=3	i=4	i=5	i=6 (réserve)
j=0 (Nord)	4	4	4	4	4	4	0
j=1 (Sud)	4	4	4	4	4	4	0

proc reinitialiser {ref_jeu} {
  upvar $ref_jeu jeu
  global joueur_en_cours
  foreach j {0 1} {
    foreach c {0 1 2 3 4 5} {
      set jeu($j,$c) 4
    }
    set jeu($j,6) 0
  }
  afficher_jeu jeu
  set joueur_en_cours 1
  afficher_joueur_en_cours $joueur_en_cours
}

La routine suivante réalise véritablement le mouvement proposé, en distribuant les graines extraites d’un trou. Il s’agit probablement de la fonction nécessitant le plus d’adaptation d’un jeu à l’autre. N’oublions pas qu’elle doit renvoyer une valeur négative si le mouvement indiqué conduit à une position inacceptable (dans d’autres circonstances cela pourrait représenter une mise en échec-au-roi).

proc effectuer_mouvement {ref_jeu joueur mvt} {
  upvar $ref_jeu jeu
  set j $joueur
  set c $mvt
  set nb $jeu($joueur,$mvt)
  set jeu($joueur,$mvt) 0
  if {$nb < 1} {return -1}
  while {$nb > 0} {
    incr c
    if {$c > 5} { # Passage de l'autre côté
      set c 0
      set j [expr 1 - $j]
    }
    if {($c != $mvt) || ($joueur != $j)} {
      # on saute le trou de départ
      incr nb -1
      incr jeu($j,$c)
    }
  }
  if {$j != $joueur} { # captures dans le terrain adverse
    while {$c >= 0} {
      if {($jeu($j,$c) < 2) || ($jeu($j,$c) > 3)} { break }
        incr jeu($joueur,6) $jeu($j,$c)
        set jeu($j,$c) 0
        incr c -1
    }
  }
  # il faut laisser au moins une graine chez l'adversaire
  set j [expr 1 - $joueur]
  foreach c {0 1 2 3 4 5} {
    if {$jeu($j,$c) > 0} {return 0}
  }
  return -1
}

Nous avons invoqué précédemment une routine partie_terminee, qui vérifiera simplement si un joueur a atteint les vingt-quatre graines en réserve.

proc partie_terminee {ref_jeu} {
  upvar $ref_jeu jeu
  if {($jeu(0,6)>=24) || ($jeu(1,6)>=24)} {return 1}
  return 0
}

Enfin, avant d’aborder l’interface graphique du jeu, nous devons écrire la fonction d’évaluation. Comme nous l’avons suggéré plus haut, c’est un élément crucial pour l’intelligence du système. C’est justement parce que le jeu est complexe qu’il est impossible de l’explorer intégralement et que l’on doit avoir recours à une fonction capable d’estimer avec précision l’avantage d’un joueur par rapport à l’autre.

Nous allons écrire une fonction d’évaluation simple, mais chacun pourra facilement l’adapter pour expérimenter de nouveaux paramètres. Notre routine prendra en argument le nom du joueur pour lequel l’évaluation doit être faite. En réalité, les mêmes calculs seront exécutés pour les deux joueurs, mais cet argument permettra de déterminer dans quel sens soustraire les deux valeurs obtenues.

Le premier paramètre permettant de décrire l’avantage d’un joueur est le nombre de graines qu’il a capturées. Le contenu de sa réserve va être multiplié par une valeur arbitraire (300) afin de lui donner un poids important par rapport aux autres graines présentes dans le jeu. On constate rapidement que les trous se trouvant à droite de la rangée d’un joueur ont une importance stratégique plus élevée que ceux de gauche. En effet, ils sont plus difficilement touchés par l’adversaire pour les captures, et à l’inverse offrent un accès plus facile vers le jeu de l’opposant. Nous allons donc pondérer leur contenu par une valeur croissante de gauche à droite (1, 2, 3…6).

proc evaluation_position {nom_jeu joueur} {
  upvar $nom_jeu jeu
  foreach j {0 1} {
    set evaluation($j) [expr 300 * $jeu($j,6)]
    foreach i {0 1 2 3 4 5} {
      set n $jeu($j,$i)
      incr evaluation($j) [expr $n * ($i + 1)]
    }
  }
  return [expr $evaluation($joueur) - $evaluation([expr 1 - $joueur])]
}

Lorsqu’on veut écrire une fonction d’évaluation, il est difficile de savoir où s’arrêter. Nous n’avons pris en considération que les paramètres les plus évidents. D’autres pourraient également être utilisés (« y a-t-il des graines menacées de capture ? », « dispose-t-on de greniers suffisants pour faire deux fois le tour du jeu ? », etc.) Le problème est d’arriver à distinguer les éléments qui relèvent véritablement de l’évaluation et ceux qui tentent de prévoir les coups suivants. Vérifier si des graines sont menacées de capture revient simplement à essayer de repousser l’horizon de l’exploration d’un demi-coup supplémentaire.

Notons que l’on se rapproche du domaine de l’apprentissage automatique, et que l’on pourrait imaginer un système où la fonction d’évaluation évoluerait en s’appuyant sur les mécanismes auto-adaptatifs habituels (réseaux connexionistes, algorithmes génétiques, etc.), d’autant que le nombre de paramêtres d’entrée dans le jeu d’Awélé est relativement restreint.

Interface graphique

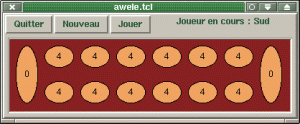
Pour construire l’interface graphique de notre programme, nous nous appuyons sur la bibliothèque Tk. Ceci nous permettra de réaliser une interface tout à fait acceptable en quelques lignes de code. La première procédure sert à construire la fenêtre du jeu.

proc creer_fenetre {ref_jeu} {
  global widget
  pack [frame .f -relief raised -bd 2]
  pack [frame .f.b ] -fill x
  pack [button .f.b.quitter -text "Quitter" -command {exit}] -side left
  pack [button .f.b.reinit -text "Nouveau"  -command "reinitialiser $ref_jeu"] -side left
  pack [button .f.b.jouer -text "Jouer"     -command "ordinateur_joue $ref_jeu"] -side left
  pack [label .f.b.txt -text "Joueur en cours : Sud"]
  pack [frame .f.d -relief sunken -bd 1] -fill both -expand 1 -padx 5 -pady 5
  pack [canvas .f.d.c -relief sunken -bd 1 -height 100 -width 390 -background brown4]
  for {set j 0} {$j < 2} {incr j 1} {
    for {set c 0} {$c < 6} {incr c 1} {
      set x1 [expr 50 + 50 * $c]
      set y1 [expr 10 + 50 * $j]
      set x2 [expr 90 + 50 * $c]
      set y2 [expr 40 + 50 * $j]
      set xt [expr 70 + 50 * $c]
      set yt [expr 25 + 50 * $j]
      if {$j > 0} {set i $c} else { set i [expr 5 - $c] }
      .f.d.c create oval  $x1 $y1 $x2 $y2 -fill SandyBrown -tags "jeu($j,$i)"
      set widget($j,$i) [.f.d.c create text $xt $yt -anchor center -tags "jeu($j,$i)"]
      .f.d.c bind "jeu($j,$i)" <Button> "humain_joue $ref_jeu $j $i"
    }

    set x1 [expr 10 + 340 * $j]
    set x2 [expr 40 + 340 * $j]
    set xt [expr 25 + 340 * $j]
    .f.d.c create oval  $x1 10 $x2 90 -fill SandyBrown
    set widget($j,6) [.f.d.c create text  $xt 50  -anchor center]
  }
}

Les premières lignes de cette routine créent une barre de boutons en haut de l’écran, pour quitter, réinitialiser le jeu, ou pour demander à l’ordinateur de joueur le coup suivant. Ensuite, une zone de dessin (canvas) est remplie avec des ovales représentant les trous et les réserves, ainsi que des zones de texte indiquant le contenu des trous. Ces zones de texte sont référencées par le tableau de variables globales widget(), que nous mettrons à jour dans les routines ci-dessous. L’instruction bind permet d’associer une action (humain_joue) à un évènement (pression d’un bouton de la souris). Les deux routines suivantes servent à afficher l’état des trous. Pour indiquer le dernier coup joué par l’ordinateur, le texte représentant le contenu de la case jouée passera en rouge.

proc afficher_jeu {ref_jeu} {
        upvar $ref_jeu jeu
        global widget
        for {set j 0} {$j < 2} {incr j 1} {
                for {set i 0} {$i <= 6} {incr i 1} {
                        .f.d.c itemconfigure $widget($j,$i) -fill black
                        .f.d.c itemconfigure $widget($j,$i) -text $jeu($j,$i)
                }
        }
}
proc indiquer_coup_joue {joueur coup} {
        global widget
        .f.d.c itemconfigure $widget($joueur,$coup) -fill red
}

Enfin, les deux dernières routines de l’interface graphique affichent respectivement le nom du joueur attendu, et les résultats de la partie.

proc afficher_joueur_en_cours {joueur} {
        if {$joueur} { set nom Sud } else { set nom Nord }
        .f.b.txt configure -text "Joueur en cours : $nom"
}
proc afficher_resultats {ref_jeu} {
        upvar $ref_jeu jeu
        afficher_jeu jeu
        if {$jeu(0,6) == $jeu(1,6)}  { set msg "Match nul !"}
        if {$jeu(0,6) >  $jeu(1,6)}  { set msg "Joueur Nord gagne !"}
        if {$jeu(0,6) <  $jeu(1,6)}  { set msg "Joueur Sud gagne !"}
        tk_messageBox -message $msg -title "Résultat" -type ok
}

Fonctions centrales

Voyons pour terminer les instructions centrales du programmes, celles qui vont invoquer les routines ci-dessus et initialiser les variables globales. Notre fichier général – que vous pouvez trouver intégralement sur mon site (voir paragraphe Liens) – sera :

#! /usr/bin/wish
  …routines décrites plus haut…

  set liste_mouvements {0 1 2 3 4 5}
  set erreur -100000
  set profondeur_maxi   6
  creer_fenetre jeu
  reinitialiser jeu

La variable globale profondeur_maxi permet de configurer la profondeur de réflexion, donc le niveau de jeu de l’ordinateur. La profondeur de six demi-coups permet d’avoir des résultats corrects sur une machine de capacité moyenne. Sur un processeur rapide, il est possible d’augmenter nettement cette valeur.

Conclusion

Le but de cet article n’était pas de réaliser un véritable programme champion d’Awélé, et nous en sommes loin, mais simplement de présenter les mécanismes les plus courants pour programmer des jeux de réflexion. Pour améliorer les performances d’un tel logiciel, deux pistes peuvent être suivies :

augmenter la profondeur de la recherche : pour cela il faut améliorer les performances du programme afin de conserver un temps de réponse acceptable. On l’optimisera donc en l’écrivant dans un langage compilé par exemple ;
améliorer l’intelligence du système : cela s’obtient en travaillant sur la fonction d’évaluation, en recherchant les paramètres les plus pertinents, et en comparant les résultats. Il peut être intéressant d’opposer automatiquement plusieurs versions de fonction d’évaluation en les faisant joueur les unes contre les autres.

L’implémentation en Tcl est amusante, mais n’est évidemment pas suffisament efficace pour un véritable programme de jeu de réflexion. L’avantage de ce script est de pouvoir modifier très facilement les paramètres et la fonction d’évaluation, avant d’en écrire une dans un langage compilé plus rapide. On notera malgré tout que le langage Tcl, associé à la bibliothèque Tk permet d’implémenter un jeu complet avec une interface utilisateur graphique en utilisant seulement 200 lignes de code environ !

Bibliographie

[BLAESS 2001] Christophe Blaess « Langages de Scripts sous Linux » Editions Eyrolles 2001.
[GOLDSCHLAGER 86] Les Goldschlager & Andrew Lister « Informatique et Algorithmique » InterEditions 1986. Traduction par Virginie Sumpf, titre original « Computer Science: A Modern Introduction«
[WINSTON 92] Patrick Henry Winston « Artificial Intelligence Addison-Wesley 1992.

Liens

Le script complet : https://www.blaess.fr/christophe/logiciels/src/awele.tcl
Les règles de l’Awélé, ainsi qu’une applet Java qui implémente un jeu d’Awélé employant probablement la même fonction d’évaluation que nous, car les niveaux de jeu sont à peu près équivalents (mais plus rapide en Java qu’en Tcl !) :http://www.sdv.fr/pages/casa/html/awele.html

URL de trackback pour cette page

Christophe Blaess